Михаил Александрович Петров, ФГАОУ ВО «Московский политехнический университет»,
факультет машиностроения, кафедра «Обработка материалов давлением и аддитивные технологии»

С появлением технологий послойного нанесения материалов стало возможным изготавливать особо сложные изделия, содержащие внутренние каналы, нависающие элементы, сложные отверстия и другие элементы, создания которых ранее приходилось избегать. Без наличия цифровых инструментов и современных компьютеров изготовление таких изделий просто невозможно, так как вся технология изготовления формируется на компьютере, с использованием программного обеспечения. В связи с этим стало возможным сменить подходы в проектировании изделий и обратиться за помощью при их разработке к природе и её законам, миллионами лет оттачивавшей мастерство в создании объектов флоры и фауны.
Одним из наиболее востребованных и интересных крупных направлений исследования в технике является направление по снижению веса изделия. На рис. 1 представлены две ветви, одна из которых связана с разработкой новых материалов с низкой плотностью, из которых изготовлен объект, а другая связана с геометрической оптимизацией конструкции объекта [1].
Рис. 1. Основные направления работ по снижению веса изделий
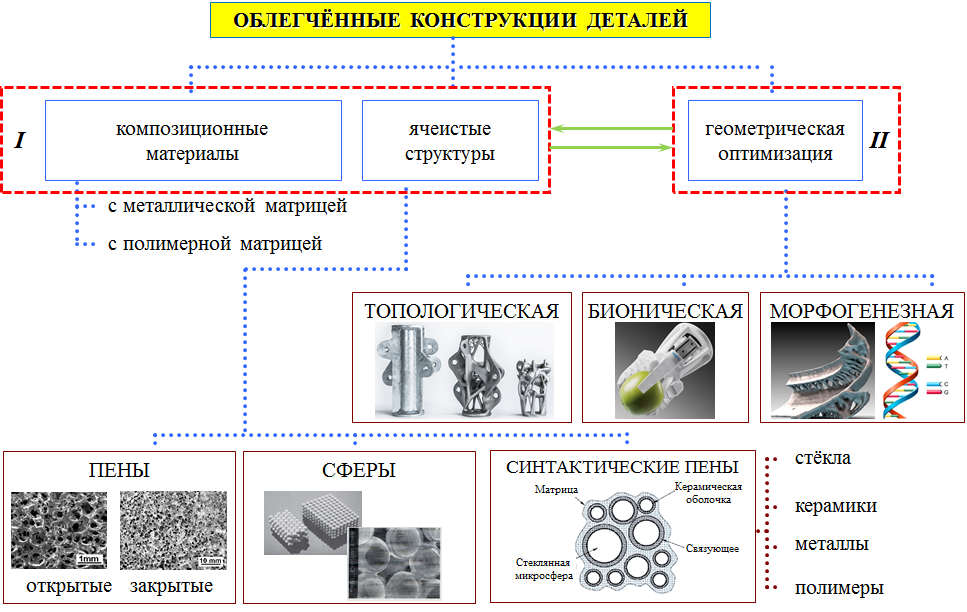
Естественно, что подходящим вариантом решения оптимизационной задачи для каждого отдельного случая будет такое решение, при котором будет выполняться построение формы по заданной целевой функции (масса, жёсткость, напряжение, частота и т.д.). Рассмотрим более подробно вторую ветку. Как видно, в неё включены три оптимизационные задачи: топологическая, связанная с оптимальным распределением материала по заданному объёму, бионическая, аналогична топологической, но имеет аналог в живой или неживой природе, и морфогенезная, позволяющая синтезировать форму с учётом временных изменений в материале и окружающих условиях эксплуатации, является неким аналогом ДНК, программы, по которой, согласно сегодняшним данным науки, происходит развитие всех живых организмов, формирование их внешнего облика.
В свою очередь, топологическую оптимизацию можно классифицировать более детально по целевым функциям или способам удаления материала из рассматриваемого объёма: топографическая (оптимизация формы граней, свойственна для повышения частоты собственных колебаний конструкции), свободная (оптимизация поддержек нависающих частей, свойственна для сильно выступающих и ветвящихся конструкций), размерная (оптимизация толщины элементов конструкции, свойственна для выбора толщины листовых конструкций), ячеистая (замена сплошного материала на периодическую структуру с дальним или ближним порядком расположения элементарных ячеек, например, по периодическому, фрактальному или стохастическому алгоритмам; характерно для ферменных конструкций, конструкций с высокой вибро- и шумоизоляцией, и энергопоглощающей способностью). Зачастую топологическую оптимизацию выделяют отдельно, подразумевая при этом оптимизацию в рамках большего объёма, из которого необходимо удалить материал, по сравнению, например, с топографической или размерной оптимизацией.
Известная стандартная процедура по проектированию изделий на основе результатов расчётов нашла в XXI веке симбиотическое воплощение в виде программ нового класса, которые можно перевести как программы для проектирования на основе результатов компьютерного моделирования (Computer Aided Engineering Design, или CAED, а также simulationdriven design, performance driven design). С их помощью стало возможным совмещение нескольких компетенций проектировщика изделия, а именно — разработка геометрии и численные расчёты. Воплощая в жизнь данный подход, мы смогли получать конструкции деталей, напоминающие по форме природные аналоги, обходить при проектировании строгие линии, образующие резкие переходы, углы, учитывать большую вариативность кривизны поверхности, реализовывать плавные, гладкие переходы между поверхностями. На первый взгляд, отражение в производственной среде должно бы найти резкий негативный отклик на такой подход, так как производственные машины не могут гарантировать проработку того или иного оформления сопряжений поверхностей. Но это не так, потому что с развитием машиностроения происходит становление как технологий, так и новых методик. Как и у медали, у каждой новой технологической ветки есть две стороны. В современном наборе аддитивные технологии играют одну из ведущих ролей при изготовлении деталей любой сложности. Но при этом в связи с нехваткой лабораторной и экспериментальной информации для изготовления полностью функциональной детали, работающей в условиях многоциклового нагружения на протяжении нескольких лет, требуется информация как по усталостной прочности, так и по её эксплуатационным характеристикам при работе совместно с другими деталями в сборке. Получить такую информацию можно, либо основываясь на прямых экспериментах, либо на основе численного моделирования. Последний вариант требует большого количества данных, получаемых на основе экспериментов.
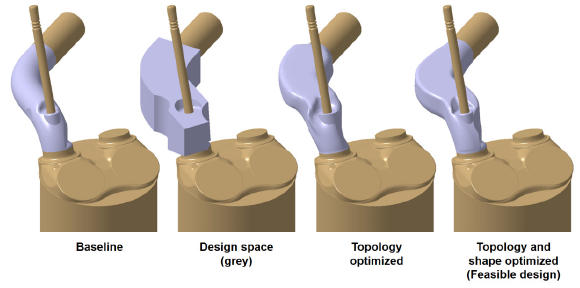
Поэтому получение абсолютно работоспособной новой детали затруднено в связи с отсутствием информации о её итоговых эксплуатационных свойствах. Однако, это не означает, что эксплуатационные свойства не могут быть определены. Накоплен огромный опыт по разным эксплуатационным нагрузкам деталей известной конструкции, образующим так называемую схему нагружения, которая и используется при проектировании новой аддитивно-ориентированной конструкции детали. Представим ситуацию, при которой существующая форма детали, гарантированная чертёжными размерами, должна удовлетворять повышенным прочностным требованиям по коэффициенту запаса (КЗ), рассчитанному, например, по пределу текучести. В этом случае проведение геометрической оптимизации формы может быть затруднено и результат не будет соответствовать ожиданиям. Теперь освободим базовую деталь от скруглений, фасок, отверстий для снижения веса и т.д., добавим избыточного материала, создавая таким образом больше возможностей программе для расчёта силовых полей её конструкции. При такой постановке программа, как скульптор, сама определит, что следует оставить, а что удалить. Показателем для этого служит КЗ, определяемый по разным целевым функциям (жёсткость, масса, частота, максимальное напряжение и т.д.). Сам подход к распределению материала по объёму имеет, уже упомянутый выше, вполне установившийся термин — топологическая оптимизация, при которой проводится поиск экстремумов целевой функции. Обращаясь к одноимённому разделу математики, стоит отметить, что топология — наука о резиновых телах, которая предполагает перераспределение материала по бесконечно упругому объёму, при этом удаление материала не подразумевается (рис. 2) [2]. Так, например, согласно допущениям, принятым в топологии, и условию неразрывности можно из множества, расположенного в форме тороидальной поверхности, получить кружку и наоборот. Но на практике реализуется другой подход, в соответствии с которым материал удаляется из тех мест, где действуют наименьшие напряжения.
Рис. 2. Примеры топологической оптимизации и морфогенезного проектирования
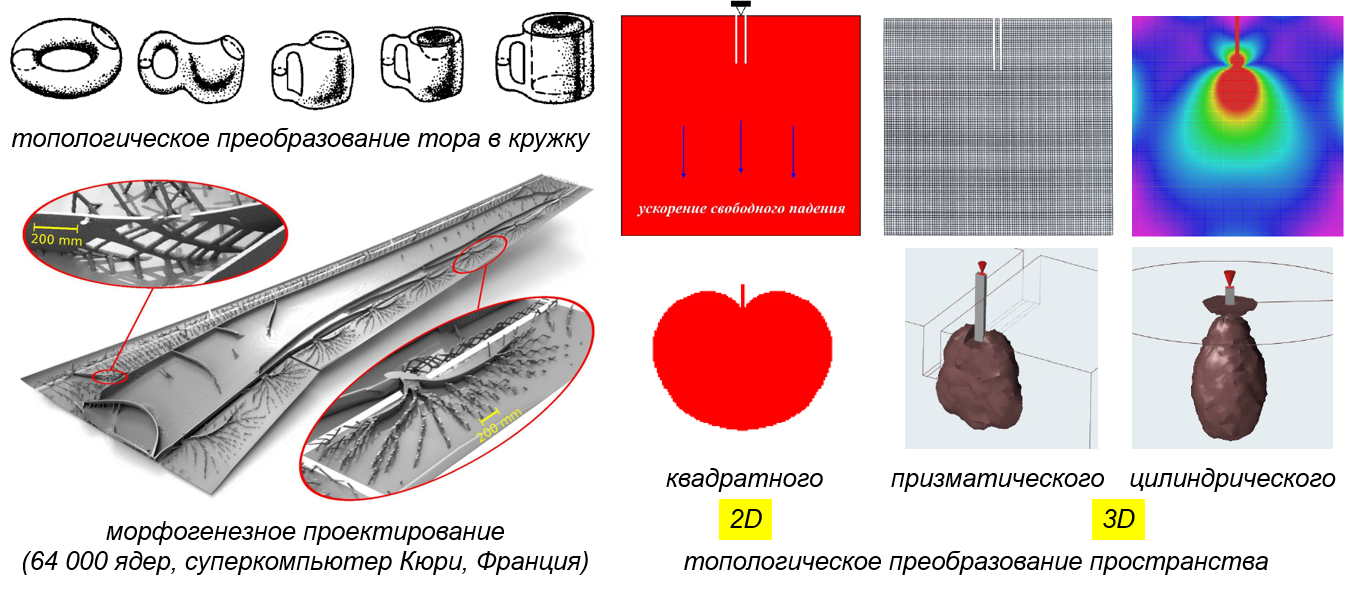
Это справедливо как для двухмерного, так и трёхмерного пространств. На примере объектов, напоминающих яблоко или грушу, на которые действует лишь ускорение свободного падения, и имеется лишь одно условие закрепления, показано, что при всех равных условиях получаемая форма зависит от геометрии избыточного, свободного объёма или его границ. Выполненное на суперкомпьютере вычисление конструкции крыла самолёта (рис. 2), работающего в режиме дозвуковых скоростей полёта, для разного угла установки крыла показало, что получившаяся геометрия непростая, имеет дискретность, а наиболее подходящим способом для изготовления такой геометрии являются аддитивные технологии [3].
Современные конструкционные материалы пока ещё не позволяют в полной мере реализовать подход о перераспределении материала без его разрушения. Так, например, известны конструкции самолётов с изменяемой стреловидностью крыла (КИС), появившиеся лишь в середине XX века, причём для некоторых из них изменение стреловидности допускается перед взлётом, но не во время полёта. Однако для полной трансформации фюзеляжа самолёта, для создания схемы нагружения сообразно возникающим нагрузкам при полёте, например, в режиме гиперзвукового полёта, имеющихся знаний о материалах и производственных технологий явно недостаточно. На рис. 3 показан кадр из кинофильма «Полёт навигатора» (1986 года), наглядно иллюстрирующий эту идею.
Рис. 3. Изменение формы летающего объекта согласно режиму полёта [4]


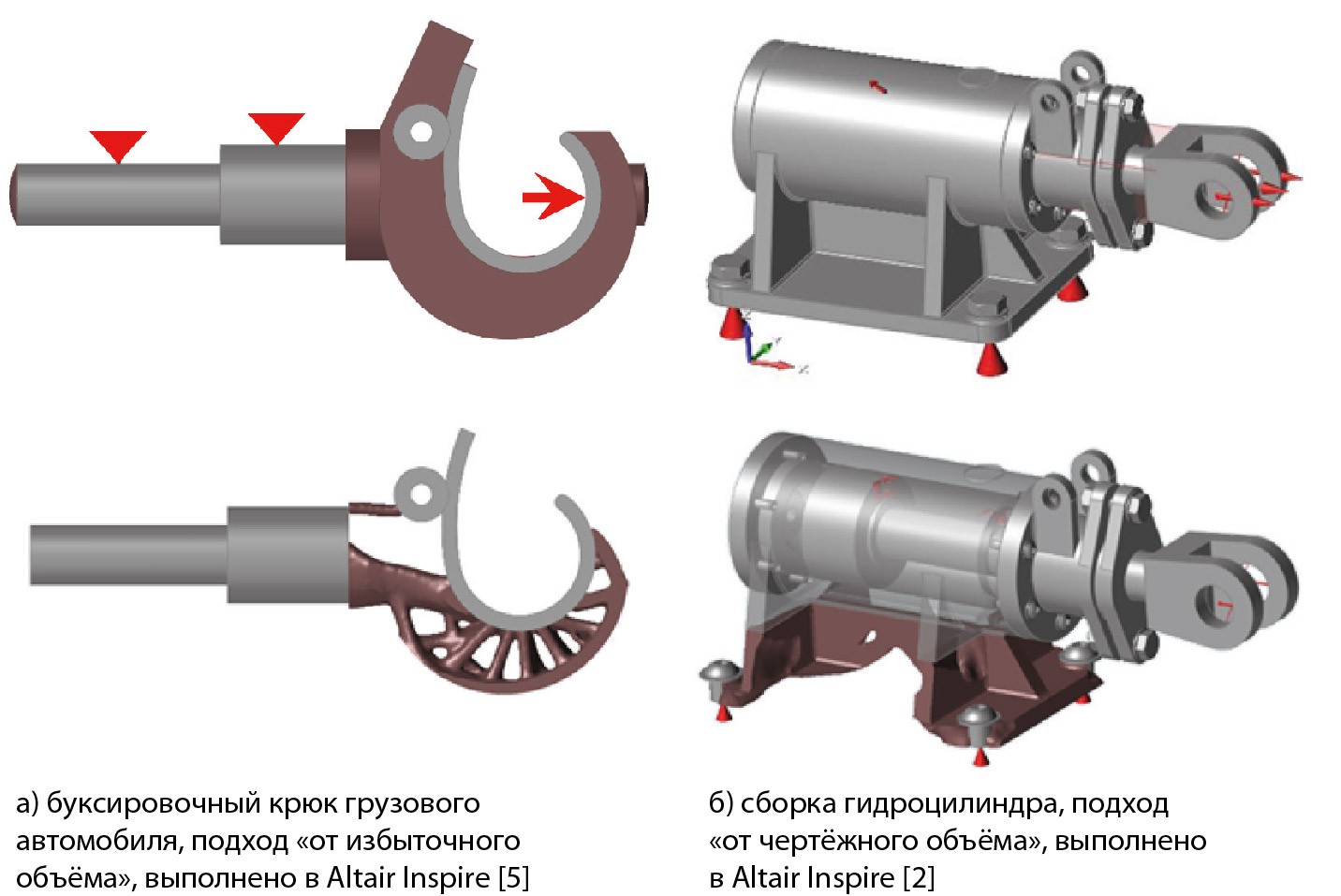
В зависимости от того, в каком направлении происходит движение, т.е. от «избыточной» геометрии формы к оптимизированной (рис. 4а) или от имеющейся геометрии формы, заданной геометрическими размерами, к оптимизированной (рис. 4б), а также от того, учитывается ли влияние возможностей производственных процессов, существуют собственные имена этих подходов. Например, на сегодняшний день формируется определение генеративного проектирования, которое рассматривает всестороннее влияние факторов на внешнюю геометрию изделия, включая и особенности производственного процесса. Сама получающаяся биоподобная форма детали порождает термин бионическое проектирование. Куда более продвинутым является термин морфогенезное проектирование, которое рассматривает конструкцию детали, как порождаемую не только на основании схемы нагружения, но и изменяемую на основании эксплуатационных свойств.
Рис. 4. Примеры топологической оптимизации с указанием схем нагружения: по «избыточному» объёму (а) и по детали согласно чертежу (б)
На рис. 5 показаны реальные ферменные конструкции архитектурных элементов железнодорожных станций, в которых применена ячеистая оптимизация по фрактальному алгоритму. Мировую известность также приобрели такие сооружения, как Шуховская башня (г. Москва, Россия), Эйфелева башня (г. Париж, Франция) и храм Святого семейства Саграда Фамилия (г. Барселона, Испания). При сравнении с имеющимися в природе аналогами можно установить однозначную взаимосвязь, например, с ветвью соцветия капусты брокколи или кроной дерева.
Рис. 5. Примеры ячеистой оптимизации в архитектуре
а) дебаркадер Витебского вокзала (г. Санкт-Петербург) [4]

б) навес перрона Ленинградского вокзала (г. Москва) [6]

в) капуста брокколи [4]

в) фрактальные зонтичные деревья и кроны [7]
На схеме рис. 6 приведена некоторая классификация задач, или методика перепроектирования изделия под технологии аддитивного производства. Вводится условие, относительно которого и выстраивается дальнейшая методика проектирования. Для деталей, являющихся прототипами серийных изделий, стоимость второстепенна, а на первом месте находятся преимущества, достигаемые в ходе эксплуатации прототипа, что является его доминантой, которая позволяет вызвать интерес к продукту, привлечь инвестиции на его промышленное освоение.
Рис. 6. Блок-схема перепроектирования изделий [8]
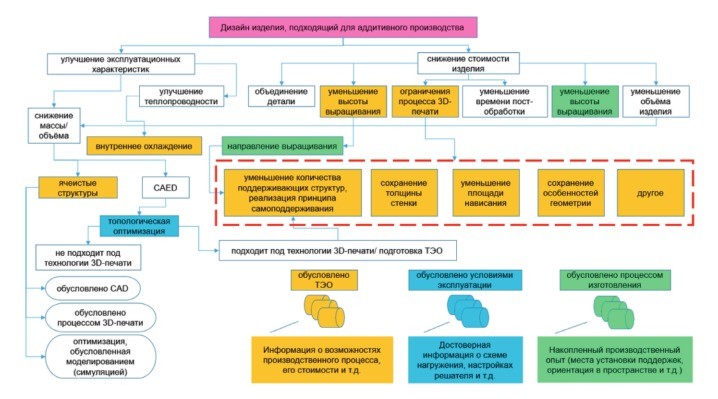
Улучшение теплопроводности — один из показателей, который может быть заменён на интересующее ключевое эксплуатационное свойство, например, сопротивление высокотемпературной ползучести. Стоимость изделия также является многопараметрической задачей. При этом на рисунке показано лишь влияние производственных издержек, непосредственно связанных с реализацией процесса, и не показано внешнее воздействие, вызывающее повышение цены, например, в результате труднодоступности исходного сырья или инфляции.
Реализация многих ключевых блоков, отмеченных цветом, требует наличия информации конструкторско-исследовательского характера. Согласно данным статьи [8], стоимость одного грамма детали в зависимости от её сложности после геометрической оптимизации варьируется от 3 до 7 евро/грамм при единичном производстве. Существующее программное обеспечение позволяет получить разнообразную геометрию, но не готово со стопроцентной вероятностью гарантировать работоспособность того или иного исполнения детали. При возникновении рекламационных споров сторона-производитель будет искать причину поломки детали в неправильных условиях эксплуатации, а потребитель — в бракованном изделии, в нарушении технологического процесса производства.
Как ни парадоксально, но обе стороны окажутся правы, так как одна сторона не в полном объёме сформулировала техническое задание, в которое включены возможные отклонения от базовой схемы нагружения, а другая — выбрала вариант топологической оптимизации, в котором отклонения от базовой схемы нагружения не предусмотрены. В случае страхования продукции, как это обычно происходит на заготовительных производствах развитых индустриальных стран, коэффициент страхования может быть высоким в связи с высокой степенью риска потенциально эксплуатационно бракованной детали. В таком случае применяют подходы мелкосерийного или единичного производства, позволяющие опробовать прототипы в работе и определить степень их надёжности. Однако, в этом случае речь скорее идёт об опытно-конструкторских работах (ОКР), а не о производственных сериях, о количестве изделий значительно куда более скромном.
На сегодняшний день весь спектр задач, связанных с топологической оптимизацией изделия, является опытным, требует тщательной проработки на предмет взаимозаменяемости с деталями старых конструкций. Понимание этой проблемы позволит более прогрессивно продвигаться в направлении оптимальной конструкции детали новой формы. В современной практике конкурентную борьбу ведут несколько крупных разработчиков программного обеспечения (ПО) топологической оптимизации, основной целью которых является предоставить быстрый инструмент для проектирования большого числа вариантов исполнения конструкции детали после геометрической оптимизации. Разработчики ПО уделяют внимание дружелюбности интерфейса ПО и быстроте расчётов. Топологическая оптимизация может быть проведена либо для одной детали в условиях статического или динамического нагружения, либо для нескольких деталей, включая сборки.
В таблице 1 представлены программы для проведения геометрической оптимизации. Все перечисленные программные продукты являются проприетарными или коммерческими. Для академических целей многие из них предоставляются бесплатно исключительно для обучения, а не получения коммерческой выгоды.
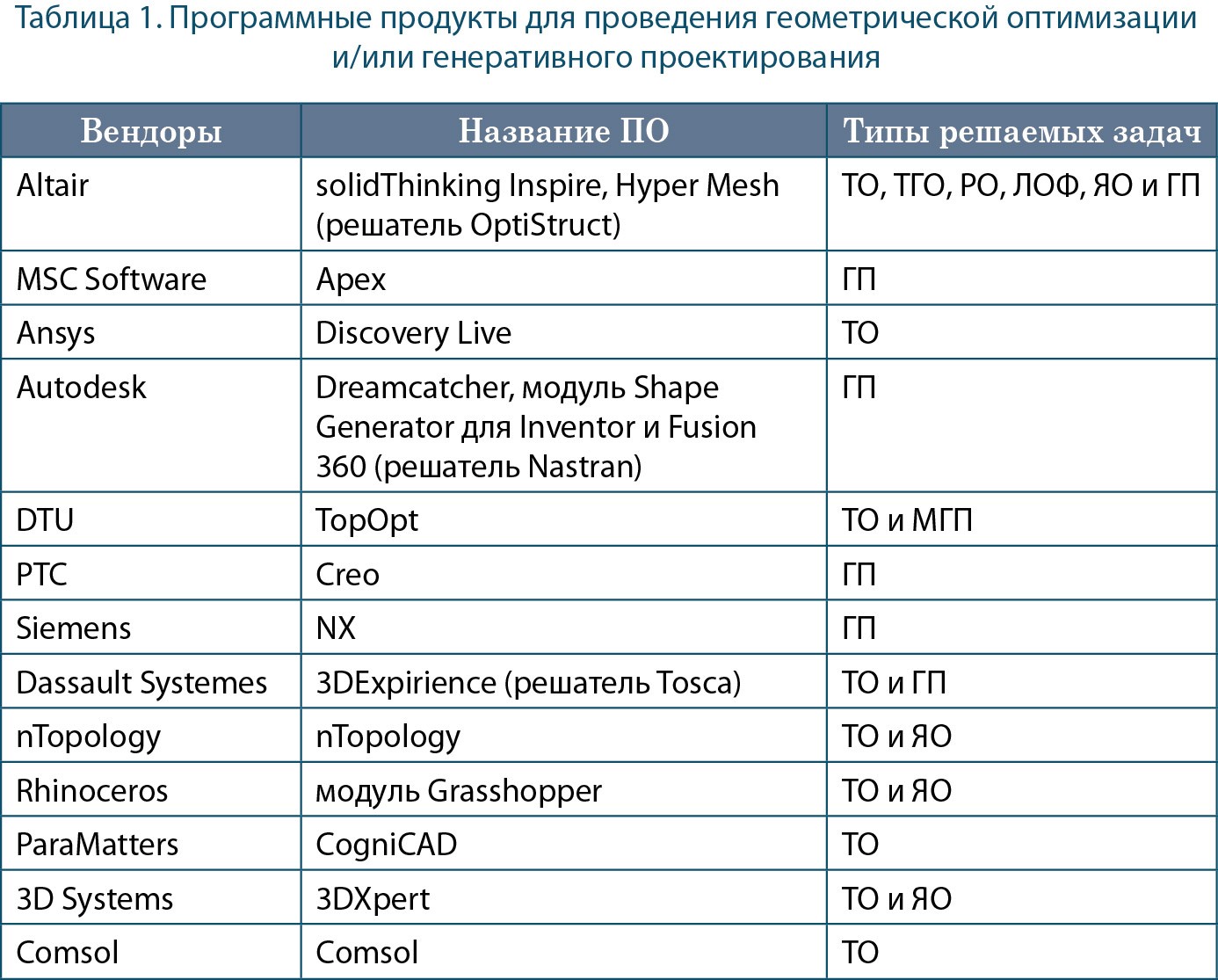
Основные типы решаемых задач: топологическая оптимизация (ТО), топографическая оптимизация (ТГО), размерная оптимизация (РО), локальная оптимизация формы (ЛКФ) и ячеистая оптимизация (ЯО), генеративное проектирование (ГП) и морфогенезное проектирование (МГП). На рис. 7 представлены некоторые примеры результатов геометрической оптимизации машиностроительных (а, в–е), спортивных (б) и архитектурных изделий (ё, ж).
Рис. 7. Примеры геометрической оптимизации
а) диск колеса микроавтобуса VW и задняя вилка мотоцикла, выполнено в Autodesk Fusion 360 [12]


б) баскетбольная стойка, выполнено в Altair OptiStruct/Inspire [13]

в) кронштейн, выполнено в Dassault Systemes 3DExpirience [14]

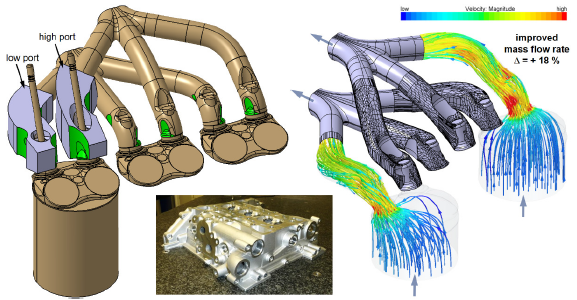
г) усовершенствование канала впускного и выпускного коллектора ДВС, выполнено в Dassault Systemes 3DExpirience [15]
д) этапы изменения рамы навесного оборудования сельскохозяйственной машины (слева) и установленный элемент после изготовления по второму варианту (справа), выполнено в Altair OptiStruct/Inspire совместно с компанией Amazone [16]
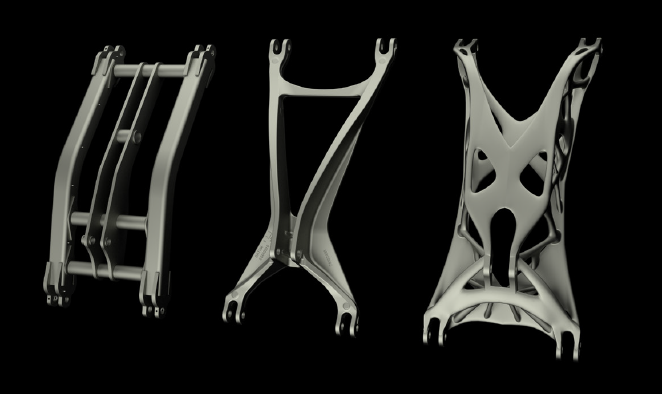

е) коленчатый вал ДВС, разработанный инженерами компании Honda, выполнено компаниями Autodesk и Honda [17]

ё) архитектурный элемент после геометрической оптимизации, выполнено в Altair OptiStruct и Materialize совместно с компанией Renishaw [18]

ж) геометрическая оптимизация моста «Золотые врата», выполнено в Autodesk Fusion 360 [19]
Структурные элементы трансмиссии и шасси могут быть изменены и более точно спроектированы по возникающим внутри силовым линиям (рис. 7а). Оптимизация геометрии внутренней части коллекторов двигателя внутреннего сгорания (ДВС) позволяет повысить его проходную способность на 18% и таким образом снизить износ внутренней части коллекторов, исключив области турбулентного течения, и повысить общее КПД двигателя (рис. 7г). Также КПД ДВС может быть увеличена за счёт снижения массы деталей двигателя, например, коленчатого вала (рис. 7е). Вес различных кронштейнов (рис. 7в, ё) может быть существенно снижен как за счёт топологической оптимизации, так и за счёт введения ячеистых структур.
Рис. 7. Примеры геометрической
оптимизации (продолжение)

ж) геометрическая оптимизация моста
«Золотые врата», выполнено
в Autodesk Fusion 360 [19]
Большеразмерные изделия, такие как баскетбольная стойка (рис. 7б), структурный элемент навесного оборудования для уборочной техники (рис. 7д) или даже автодорожный мост (рис. 7ж), не оказывают принципиально никакого влияния на устойчивую работу алгоритмов геометрической оптимизации, но требуют мощных вычислительных систем (суперкомпьютеров). К наиболее известным алгоритмам топологической оптимизации можно отнести алгоритмы эволюционной одно- или двухсторонней структурной оптимизации (evolutionary structural optimization (ESO) или bi-directional evolutionary structural optimization (BESO)), которые позволяют удалять материал детали, линии и поля действия приложенных нагрузок в котором отсутствуют [9, 10].
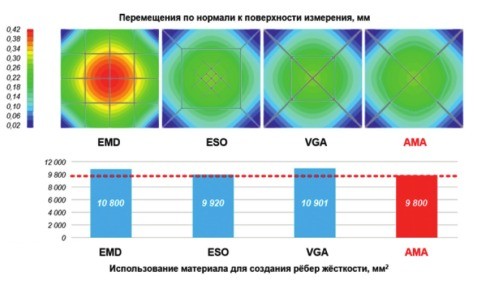
Однако из создаваемого разнообразия вариантов геометрии можно отметить и другие алгоритмы, такие как адаптивный морфогенезный алгоритм (adaptive morphogenesis algorithm (AMA), алгоритм развития жилкования (venation growth algorithm (VGA) и метод эмпирического проектирования (empirical design method (EDM), позволяющие улучшить или, наоборот, ухудшить жёсткость тонкостенных оболочечных изделий, которые более подробно описаны в статье [11].
Наиболее хороший результат был получен по алгоритму AMA, в соответствии с которым и расход материала на рёбра жёсткости, и перемещения были минимальными (рис. 8).
Рис. 8. Расход материала и результаты моделирования прогиба пластин
Выводы Для выбора наиболее правильного варианта исполнения детали из создаваемого разнообразия вариантов геометрии необходим помощник, например, на базе искусственного интеллекта (ИИ), который бы выделял варианты исполнения, подходящие для применения в машине по совокупности эксплуатационных характеристик всей сборки. Геометрическая оптимизация на базе известных алгоритмов, например, ESO или BESO, является успешной и многообещающей. Она проводится для товаров с высокой добавленной стоимостью, аэрокосмического сектора, кораблестроения и других, но постепенно распространяется и на более доступные гражданские направления, например, спортивную экипировку и инвентарь, автомобилестроение, сельское хозяйство и т.д., что позволяет сделать жизнь людей более комфортной










