Денис Кондратьев, руководитель направления «Аддитивное производство», «КАДФЕМ Си-Ай-Эс»

Для чего это нужно?
Ни для кого не секрет, что 3D-печать металлом является одной из наиболее перспективных областей для получения изделий без последующей доработки. Преимуществом аддитивного производства является большая гибкость при создании сложной геометрии с минимальным сроком проектирования и коэффициентом использования материала. Однако основной проблемой при использовании деталей, созданных с помощью 3D-печати, является их последующая квалификация и сертификация. Для корректного определения типа детали она должна быть напечатана без проблем и ошибок, а также обладать механическими свойствами, которые будут соответствовать требованиям эксплуатации. Механические свойства любой напечатанной детали основаны на характеристиках затвердевшей микроструктуры материала, а именно — на размере и типе зерна, его текстуре и присутствующих фазах. В свою очередь, изменчивость микроструктуры из-за различных условий технологического процесса порождает неоднородные изменения механических свойств детали. И это создает ограничения на предсказуемость свойств. Идентификация упомянутых изменений и их корреляция с механическими свойствами через эксперимент является длительным процессом, требующим достаточной базы экспериментов. Это не только увеличивает время производственного цикла, но и требует огромных ресурсов, а также финансов. С помощью инструментов
прогнозирования и моделирования эти изменения можно предсказать, а полученные результаты использовать для оценки механических свойств детали перед печатью. Это упростит процесс принятия решений, поскольку могут быть выбраны подходящие параметры технологического процесса. В основе изменений микроструктуры лежит размер зерен. На него влияет тепловой градиент и скорость затвердевания, которые образуют разную текстуру при различных схемах сканирования и образования вредных фаз во время охлаждения. Примером, показывающим это, может быть зависимость мощности лазера от скорости сканирования (рис. 1).
Понимание того, как эти паттерны влияют на свойства конечного материала, обеспечит путь для управления этими свойствами и более успешного внедрения этих методов в промышленность. Компания Ansys для решения данной задачи применяет двухмерные модели микроструктуры на основе метода клеточного автомата, так как он наиболее подходит по соотношению скорости и качества расчета. Конечно, разные методы печати оказывают свое влияние на эволюцию зерна при многослойной печати с использованием различных шаблонов сканирования и методов. Были проверены такие методы, как направленное энергетическое осаждение (DED), лазерное спекание металлов, селективное лазерное плавление (MLS/SLM) и электронно- лучевое плавление (EBM). Полученные результаты показали сильную корреляцию паттернов сканирования лазера с меняющейся ориентацией зерен.
Описание модели
Приведем метод двумерного клеточного автомата, который был разработан для моделирования морфологии зерен для многослойной печати и используется в решениях Ansys для предсказания затвердевания. Модель включает в себя фундаментальные основы затвердевания и учитывает рост зерна. Демонстрируется влияние шаблонов сканирования, температурных градиентов и скорости охлаждения на полученную микроструктуру. Для экономии вычислительного времени не учитывается внутрисистемное охлаждение. Таким образом, моделирование позволяет оценить размер и тип зерна, а также предоставляет информацию о текстуре. Результаты морфологии зерна продемонстрированы для различных схем сканирования, используемых в 3D-принтерах. Сам метод клеточного автомата — это алгоритм, описывающий пространственно- временную эволюцию физической системы с помощью детерминированного или вероятностного преобразования. В этом методе область пространства делится на конечное количество ячеек, а их состояние определяется из правил преобразования и влияния соседней ячейки на исходную.
В данной модели каждой ячейке присвоены четыре переменные:
(a) — переменная состояния определяет состояние ячейки, т. е. твердое тело, жидкость и границу раздела;
(b) — переменная ориентация представляет собой предпочтительную ориентацию роста зерна;
(с) — переменная количества зерен для того, чтобы отличить зерна друг от друга;
(d) — переменная твердой фракции, используется для отслеживания превращения жидкой ячейки в твердую.
В этой модели выбирается восемь ближайших соседей. Ячейки интерфейса определяются, если одна из 8 соседних ячеек является заполненной ячейкой. Вначале новые ядра заселяются в интерфейсные ячейки в соответствии с законом нуклеации: ∂N ∂T = –2μN (∆T) (1 – fs) (1) ∂t ∂t
Здесь N — число ядер: ∆T — тепловой градиент/общий объем охлаждения; ∂T/∂t — скорость охлаждения; μN — параметр зародышеобразования; fs — доля твердого вещества. Интерфейс ячейки может представлять границу ванны расплава и границу зерен, затвердевших внутри ванны расплава.
Рис. 1. Параметрический анализ наплавки. Результат эксперимента
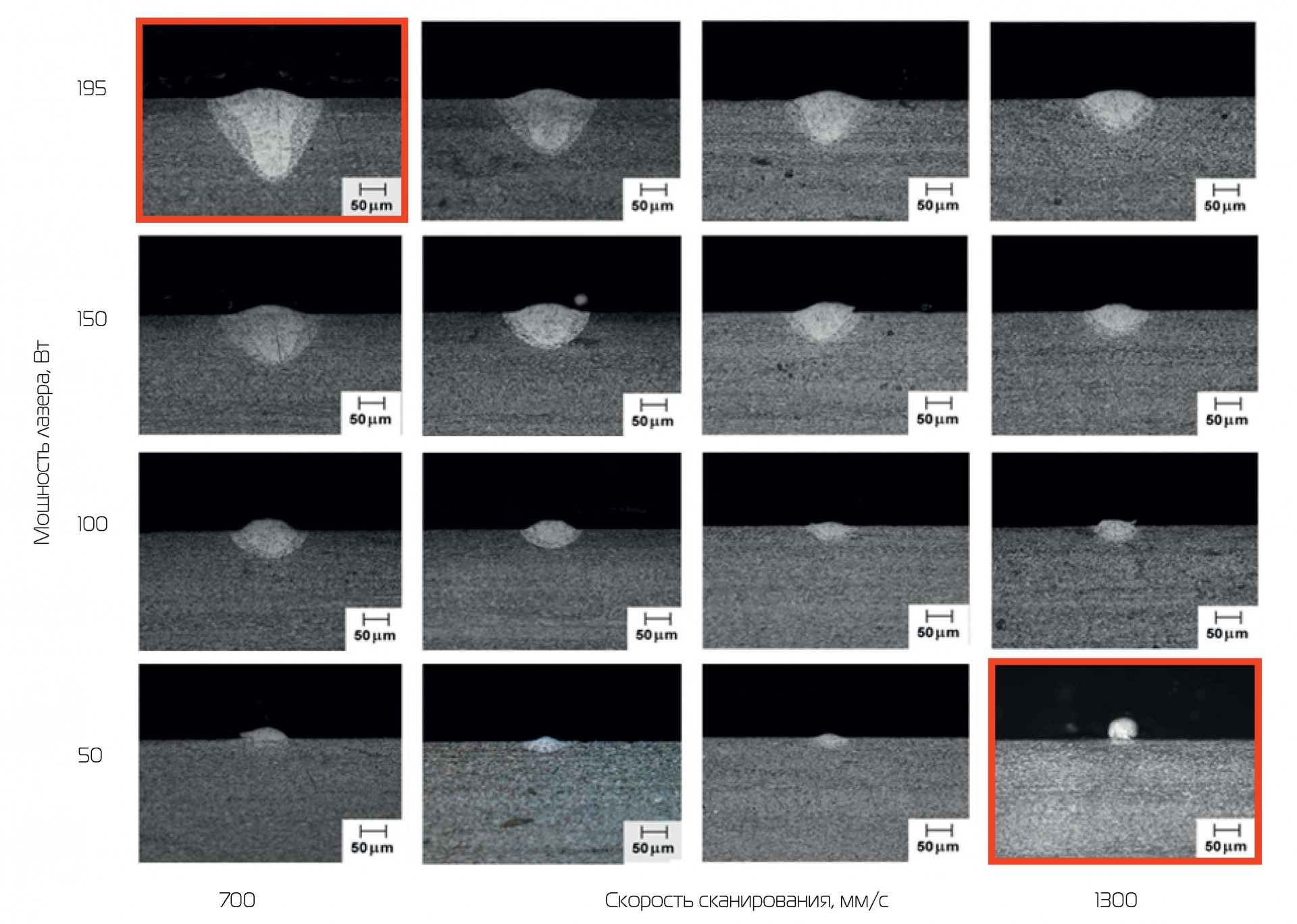
Модель зародышеобразования учитывает влияние как общего переохлаждения, так и скорость охлаждения. Вероятность зарождения клеток, расположенных на границе раздела, рассчитывается по формуле (2) для каждого временного шага: ∂N dP = NI (2) Здесь NI — общее количество ячеек, расположенных на границе раздела фаз (ванна расплава и граница зерен). Как только вероятность превышает случайное число от 0 до 1, эта ячейка переходит из жидкого состояния в твердое. После зарождения нового твердого ядра назначается предпочтительное направление роста θ0 на основе нормального угла между зародившимся ядром и движущимся источником тепла.
Движущей силой роста является количество переохлаждения, присутствующего на границе твердого и жидкого состояния материала. Скорость образования границы раздела фаз рассчитывается по формуле (3):
VN = μk (∆T) (3) Здесь μk — кинетический коэффициент границы раздела фаз; ∆T — полное переохлаждение, которое складывается из теплового переохлаждения и кривизны, вычисляемое по формуле (4):
∆T = [∆TT – ГK(tn)] (4)
Здесь ∆TT — тепловое переохлаждение; Г — коэффициент Гиббса – Томсона; K(tn) — средняя кривизна, рассчитываемая по уравнению (5): 1 fs + ∑i =1 fs (i) K = (1 – 2 ) (5) lc N +1 Здесь lc — размер ячейки; N — общее количество соседних ячеек, включая первых и вторых ближайших соседей, разделяющих границу и угол данной ячейки. В данном случае N равно 8. Для учета анизотропии скорость роста кристалла Vg в соответствии с предпочтительным ростом кристалла θ0 рассчитывается с использованием уравнения (6): Vg = VN {1 + δk cos[4(θ – θ0)]} (6) Здесь δk — степень кинетической анизотропии; θ — угол между горизонтальным направлением и нормалью к границе раздела фаз твердое тело/жидкость. Угол θ получается из градиента твердой фракции на границе раздела фаз твердое тело — жидкость. Как только скорость границы раздела получена, скорость изменения выделяющейся твердой фракции в ячейке интерфейса вычисляется с использованием уравнения (7): Vg ∆fs = G (7) lc ∆t Здесь ∆t — приращение по времени; G — геометрический фактор, относящийся к первому и второму ближайшим соседям. G, в свою очередь, рассчитывается по формуле (8):
1 G = 0,4(∑n = 1 bnI + ∑n = 1 bnII) (8)
√2 Здесь bI и bII представляют первого и второго ближайших соседей в квадратной сетке. Геометрический фактор учитывает более высокую скорость затвердевания для первых ближайших соседей по сравнению со вторыми ближайшими соседями. Если доля твердого вещества ячейки становится равной 1, то статус ячейки изменяется на твердую ячейку. Моделирование продолжается до тех пор, пока все жидкие ячейки не станут твердыми. Константы, используемые при моделировании, имеют следующие значения: — размер решетки lc = 1 мкм; — кинематический коэффициент границы раздела μk = 2 × 10–6; — коэффициент Гиббса – Томсона Г = 1,7 × 10–7; — степень кинетической анизотропии δk = 0,7; — параметр зародышеобразования μN = 103;
Допущения
Следует признать, что численное моделирование не учитывает некоторые детали. Специалист всегда держит это в уме. Так как чрезмерное погружение в детали приведет к значительному усложнению модели и возрастанию требований к расчетным нагрузкам, были приняты следующие допущения: • Не учитывается структурное переохлаждение, а общее переохлаждение на границе раздела фаз состоит из термического переохлаждения и переохлаждения по графику. • Задаются предварительно ширина и высота ванны расплава. • Считается, что зарождение происходит только на границе ванны расплава, на границе растущих зерен и в жидкой области, вдали от растущих зерен и границы ванны расплава зародышеобразование не учитывается. • Отверждение выполняется только на задней половине ванны расплава. • Источник тепла рассматривается как точечный источник внутри каждой отдельной дорожки, и его движение фиксируется смещением точечного источника. • Требуются постоянные температурные градиенты и скорость охлаждения. • Для призматической части используются основные паттерны сканирования, такие как однонаправленные, зигзагообразные, зигзагообразный с поперечной штриховкой и внешнее контурное заполнение с зигзагообразной поперечной штриховкой. • Попытки сопоставить размер зерна с к аким-либо сплавом не проводились. Результаты совпадают с точки зрения общей морфологии зерна и развития текстуры.
Рис. 2. Рост равноосных (а–в) и столбчатых (г–е) зерен при различной ориентации роста зерен.
Красный цвет — затвердевшее зерно, синий — жидкая фаза, черный — границы зерен
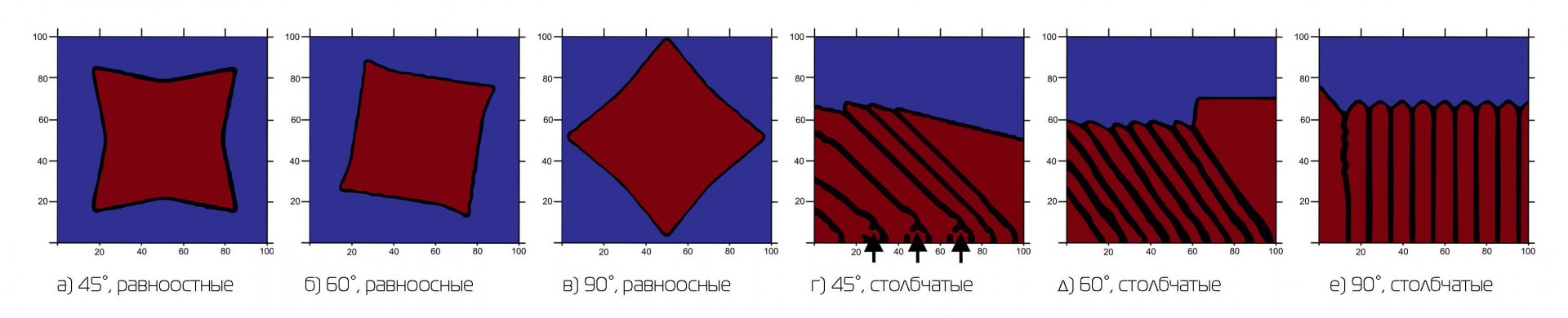
Изучался рост размера зерен вдоль предпочтительной ориентации зерен. Моделирование проводилось на различных ориентациях, таких как 45, 60 и 90 градусов. Были рассмотрены два типа роста зерен: равноосные и столбчатые. Моделирование выполнялось для 130 и 200 шагов клеточного автомата для равноосных и столбчатых зерен соответственно. Из рис. 2a видно, что зерна растут в соответствии с заданной ориентацией роста. Морфология в случае 45° и 90° практически идентична, однако асимметричная морфология может наблюдаться в случае 60°. Асимметричное поведение является обычным для методов клеточного автомата из-за анизотропии сетки. Аналогично рост столбчатых зерен также следует за предпочтительной ориентацией роста, как показано на рисунках 2г–е. Красный, синий и черный цвета представляют собой твердое тело, жидкое состояние вещества и границы зерен соответственно. В случае предпочтительной ориентации 90° и 60° все зерна расположены на одинаковом расстоянии, кроме углового (больше места для роста), однако для 45° они расположены неравномерно. В основном это связано с конкуренцией зерен между собой. На рис. 2д видно, что несколько зерен погасли на ранней стадии затвердевания (показано стрелками). В целом зерна следовали направлению своего роста в соответствии с заданной ориентацией.
Морфология зерна в зависимости от скорости источника тепла
Изменение морфологии зерен в зависимости от скорости движущегося источника тепла зафиксировано и показано на рис. 3.
Рис. 3. Изменение морфологии зерна при движении источника тепла
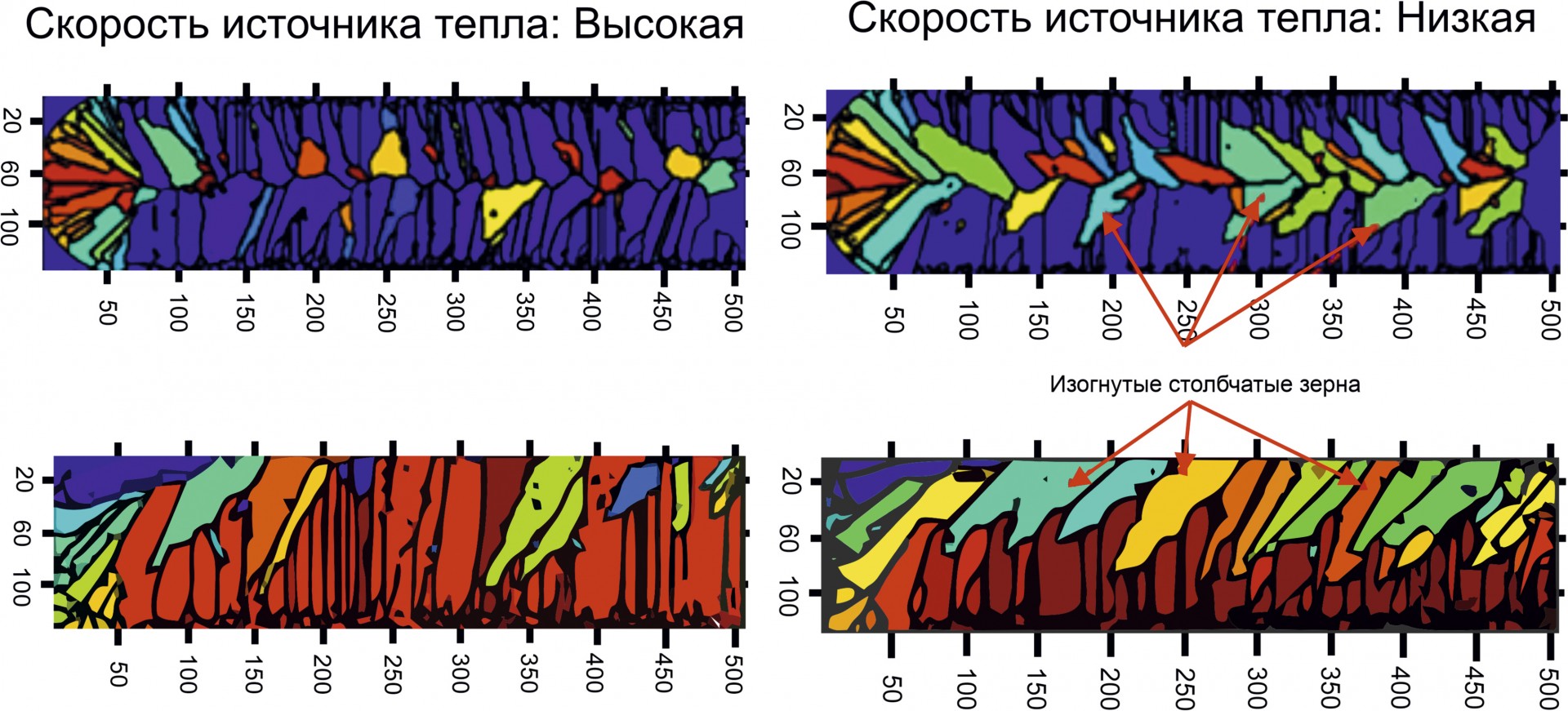
Изогнутые столбчатые зерна можно было наблюдать в плоскостях XY и YZ при более низких скоростях источника тепла по сравнению с почти вертикальными или наклонными столбчатыми зернами на более высоких скоростях. Эти типы морфологических различий зерна также наблюдаются в таких процессах, как 3D-печать с использованием лазера и сварка. Различия в морфологии зерен — прямое следствие теплового фронта и профиля ванны расплава при различных скоростях движущегося источника тепла. Во время сварки источник тепла обычно движется с меньшей скоростью, что дополнительно формирует профиль ванны расплава эллиптической формы, приводящий к образованию изогнутых столбчатых зерен. В процессах аддитивного производства лазер перемещается с высокой скоростью, образуя удлиненные профили ванны расплава, которые благоприятствуют прямому или наклонному столбчатому росту зерен. Более высокая скорость также может вызывать отсутствие плавления, но модель, представленная в этой статье, ограничивается моделированием морфологии зерна. При использовании этой модели разница может быть учтена путем изменения скорости источника тепла.
Влияние шаблона сканирования на развитие зерна
Как было сказано ранее, детали паттерна сканирования имеют большое влияние на окончательную микроструктуру. Движение источника тепла по определенной схеме сканирования важно для понимания процесса эволюции зерна.
Рис. 4. Типы шаблонов сканирования:
a) однонаправленный; б) зигзаг; в) зигзаг с поперечной штриховкой; г) наружная контурная заливка
с зигзагообразной поперечной штриховкой
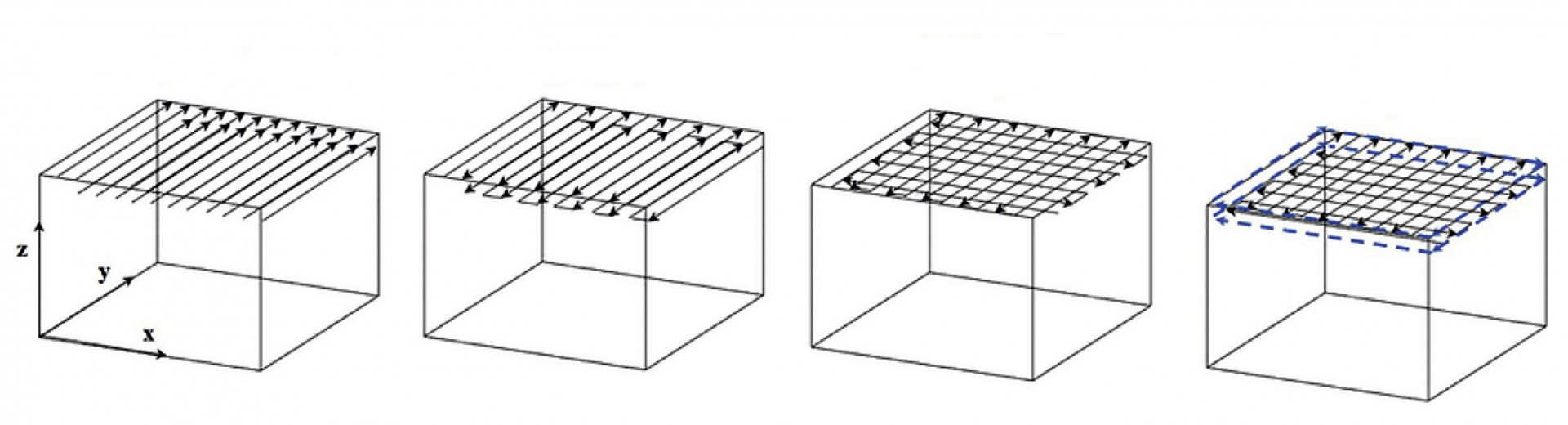
Рис. 4 иллюстрирует схему часто встречаемых шаблонов сканирования, используемых в оборудовании для аддитивного производства. Помимо этого существуют и другие типы сканирования, такие как полосы и шахматные доски, ориентированные под разными углами. Использовался постоянный температурный градиент и скорость охлаждения для моделирования эволюции зерен в SLM-процессе. Например, можно видеть график трехмерной ориентации зерна, реконструированный с использованием двухмерной ориентации зерна для одного шаблона сканирования, представленный на рис. 5. Необходимо отметить, что в процессе моделирования наблюдались значительные различия в морфологии зерен по отношению к разным плоскостям и паттернам сканирования. Работа выполнялась с использованием сплава Ti6Al4V и применением метода селективного лазерного спекания. Из рис. 6 видно, что существует сходство структуры зерен между полученными результатами моделирования и экспериментальными данными. Их результаты также показали зигзагообразный паттерн с зернами, ориентированными в одном направлении при двунаправленном сканировании, тогда как при однонаправленном сканировании зигзагообразный паттерн не очевиден. Различия можно оценить, рассматривая эффект переплавления ранее затвердевших слоев во время лазерной штриховки и его рост на соседних дорожках.
Рис. 5. Примеры эволюции зерен в SLM

Рис. 6. Сравнение экспериментальных данных и моделирования


Выводы
Исследование проводилось в широком спектре микроструктур, и статья не позволяет подробно описать каждый из полученных результатов. Проверялись различные технологические процессы, такие как SLM, DED и EBM. Стоит отметить, что при сканировании однонаправленным паттерном изогнутые столбчатые зерна наблюдаются при более медленном движении. Этот результат объясняет, почему сварка и аддитивное производство производят различную морфологию зерна. За счет уменьшения скорости охлаждения и температурного градиента морфология изменилась с зигзагообразной на однонаправленно ориентированные зерна, даже с использованием шаблонов зигзагообразной развертки. Используя эту модель, а также зная скорость охлаждения и температурные градиенты, можно предсказать эволюцию зерна в широком спектре вариантов технологических процессов (SLM, DED и EBM). Размеры зерен материала могут быть смоделированы благодаря вводу правильного параметра зародышеобразования для сплава. Модель выводит данные о размере зерна и ориентацию. Это очень полезно для прогнозирования окончательных механических свойств компонентов, изготовленных с помощью аддитивного производства. Сходство между смоделированными данными и экспериментальными данными позволяет сделать вывод, что моделирование на основе клеточного автомата для предсказания ориентации и размера зерен в аддитивном производстве может быть использовано для прогнозирования свойств материала.
Литература 1. Javed Akram, Pradeep Chalavadi, Deepankar Pal, Brent Stucker. Understanding grain evolution in additive manufacturing through modeling. Additive Manufacturing 21. DOI: 10.1016/j.addma.2018.03.021.










